¿Cuáles son las reglas de los ángulos?

Los ángulos son una medida de la separación en grados entre dos líneas o planos que se encuentran en un punto común. Para entender las reglas de los ángulos, es importante tener en cuenta algunos conceptos clave.
La suma de los ángulos en una línea recta es siempre igual a 180 grados. Esto significa que si tienes dos ángulos en una línea recta, sus medidas sumadas siempre serán 180 grados. Por ejemplo, si un ángulo mide 60 grados, el ángulo complementario medirá 120 grados.
En un triángulo, la suma de los tres ángulos siempre es igual a 180 grados. Esta regla es conocida como la suma de los ángulos de un triángulo. Por ejemplo, si un ángulo del triángulo mide 60 grados y otro ángulo mide 40 grados, el tercer ángulo deberá medir 80 grados para que la suma sea 180 grados.
Además, existen dos tipos principales de ángulos: ángulos agudos y ángulos obtusos. Un ángulo agudo es aquel que mide menos de 90 grados, mientras que un ángulo obtuso es aquel que mide más de 90 grados pero menos de 180 grados.
Otra regla importante es la bisectriz de un ángulo. La bisectriz de un ángulo divide ese ángulo en dos ángulos iguales. Por ejemplo, si tienes un ángulo de 60 grados y trazas una línea que lo divide en dos partes iguales, obtendrás dos ángulos de 30 grados cada uno.
En resumen, las reglas de los ángulos incluyen la suma de los ángulos en una línea recta, la suma de los ángulos de un triángulo, los ángulos agudos y obtusos, y la bisectriz de un ángulo. Estas reglas son fundamentales para comprender y resolver problemas geométricos.
¿Cuáles son las reglas de los ángulos?
Los ángulos son una parte fundamental de la geometría y es importante conocer las reglas que los rigen. Los ángulos se miden en grados y se representan con el símbolo °. Un ángulo completo tiene 360 grados, lo que significa que se extiende todo el camino alrededor de un punto.
El ángulo recto mide exactamente 90 grados y se representa con un pequeño cuadro en la parte interior del ángulo. Un ángulo agudo es aquel que mide menos de 90 grados, mientras que un ángulo obtuso mide más de 90 grados pero menos de 180 grados.
Los ángulos complementarios son aquellos que, cuando se suman, dan como resultado un ángulo recto de 90 grados. Por otro lado, los ángulos suplementarios son aquellos que, cuando se suman, dan como resultado un ángulo recto de 180 grados.
Además, los ángulos opuestos por el vértice son aquellos que tienen un vértice en común y sus lados forman una línea recta. Estos ángulos tienen la misma medida.
Otra regla importante es la ley del coseno que establece que en un triángulo, el cuadrado de uno de los lados es igual a la suma de los cuadrados de los otros dos lados, menos el doble producto de estos dos lados y el coseno del ángulo entre ellos.
En resumen, conocer las reglas de los ángulos es fundamental para resolver problemas geométricos y comprender las relaciones entre diferentes formas y figuras.
¿Cuáles son los tipos de angulos y sus características?
Los ángulos son figuras geométricas formadas por dos semirrectas que tienen un mismo punto de origen llamado vértice. Existen diferentes tipos de ángulos, cada uno con características y propiedades específicas.
El ángulo recto es aquel cuya medida es de 90 grados. Se representa con un cuadrado o una caja en la figura. Un ejemplo de ángulo recto es el que se forma en la esquina de una hoja de papel. La suma de los ángulos rectos siempre es igual a 360 grados.
El ángulo agudo es aquel cuya medida es menor a 90 grados. Se representa con una apertura estrecha en la figura. Un ejemplo de ángulo agudo es el formado por dos líneas en un triángulo equilátero.
El ángulo obtuso es aquel cuya medida es mayor a 90 grados pero menor a 180 grados. Se representa con una apertura amplia en la figura. Un ejemplo de ángulo obtuso es el formado por las manecillas del reloj a las 6 en punto.
El ángulo llano es aquel cuya medida es de 180 grados. Se representa con una línea recta en la figura. Un ejemplo de ángulo llano es el formado por una línea en el plano cartesiano.
El ángulo completo es aquel cuya medida es de 360 grados. Es equivalente a cuatro ángulos rectos. Se representa con una vuelta completa en la figura. Un ejemplo de ángulo completo es el formado por una persona girando su cuerpo alrededor de un eje.
Estos son los principales tipos de ángulos y sus características. Es importante tener en cuenta que el concepto de ángulo es fundamental en la geometría y tiene aplicaciones en diversos campos de estudio.
¿Cuál es la clasificación de los ángulos?
Los ángulos se clasifican según su medida en grados. Tenemos diferentes tipos de ángulos: agudo, recto, obtuso y llano.
Un ángulo agudo es aquel que tiene una medida menor a 90 grados. Por ejemplo, si un ángulo mide 30 grados, es considerado como agudo.
Un ángulo recto es aquel que tiene una medida de exactamente 90 grados. Si trazamos una línea recta y dividimos el ángulo en dos partes iguales, cada parte medirá 45 grados.
Un ángulo obtuso es aquel que tiene una medida mayor a 90 grados y menor a 180 grados. Por ejemplo, si un ángulo mide 120 grados, es un ángulo obtuso.
Un ángulo llano es aquel que tiene una medida de 180 grados. Si trazamos una línea recta y la dividimos en dos partes iguales, formaremos un ángulo llano.
Además de estos tipos de ángulos, también existen los ángulos complementarios y ángulos suplementarios.
Los ángulos complementarios son aquellos que, sumados entre sí, resultan en un ángulo recto de 90 grados. Por ejemplo, si tenemos un ángulo de 30 grados, su ángulo complementario será de 60 grados.
Por otro lado, los ángulos suplementarios son aquellos que, sumados entre sí, resultan en un ángulo llano de 180 grados. Si tenemos un ángulo de 60 grados, su ángulo suplementario será de 120 grados.
Estas son las principales clasificaciones de los ángulos según su medida. Es importante reconocer y entender estos conceptos para trabajar con ángulos de manera precisa y correcta.
¿Cómo se miden los ángulos ejemplos?
En matemáticas, los ángulos son medidas que se utilizan para describir la apertura entre dos líneas o superficies en un punto común. Para medir los ángulos, se utilizan diversas unidades de medida, como grados, radianes y vueltas.
La unidad más común para medir ángulos es el grado. Un grado se define como la 1/360 parte de una circunferencia completa. Por lo tanto, una circunferencia completa tiene 360 grados. Para medir un ángulo en grados, se utiliza un transportador, que es una herramienta en forma de semicírculo que tiene diferentes marcas y números para indicar los grados.
Otra unidad de medida que se utiliza para medir ángulos es el radian. El radian se define como el ángulo subtendido por un arco de circunferencia cuya longitud es igual al radio de la circunferencia. En una circunferencia completa, hay 2π radianes (donde π es una constante matemática aproximadamente igual a 3.14159). Los radianes son especialmente útiles en cálculos trigonométricos y en física.
En algunos casos, también se puede utilizar la unidad de medida de vuelta para medir ángulos. Una vuelta es un ángulo que recorre toda una circunferencia y se representa como 1. En otras palabras, una circunferencia completa equivale a una vuelta. Sin embargo, esta unidad de medida no se utiliza comúnmente en problemas matemáticos, sino que se utiliza más en navegación o dirección.
Al medir ángulos, es importante recordar que el punto de origen o referencia se suele colocar en el lado positivo del ángulo, generalmente en el sentido de las agujas del reloj. Además, los ángulos se pueden clasificar en diferentes tipos, como agudo, recto, obtuso o llano, dependiendo de su medida.
regla de angulos

Regla de medición multiángulo y de estilo lateral para azulejos de cerámica, 12 herramientas de ángulo de aleación de aluminio para arquitectos
- ❤ [Última versión] Con la herramienta angular de 6 piezas, puedes ajustar la posición de perforación a B. Marque las baldosas con precisión. Es una herramienta de medición y un posicionamiento de agujeros integrado. Esta regla de medición se pliega fácilmente y se guarda para ahorrar espacio y se puede llevar fácilmente a cualquier sitio de construcción. Es muy adecuado para medir la superficie de ladrillos, papel, piedra, baldosas de cerámica, madera y otros materiales.
- ❤ [Mejoras de materiales y diseño] La regla de medición multifunción está hecha de aleación de aluminio de alta calidad, superresistente al desgaste. Equipado con botones de metal. Son más fuertes que los botones de plástico y, por lo tanto, más duraderos. Los bordes son redondos y lisos, sin rebabas que pueden evitar lesiones. Sin procesamiento complicado.
- ❤ [Medición precisa] Nuestra regla de medición multiángulo es un instrumento ideal para medir ángulos precisos. Hay pulgadas y centímetros en la escala, todos los grabados láser no se desvanecerán ni desgastarán, incluso si usa la regla deslizante durante mucho tiempo, manténgala clara y fácil de leer para una medición precisa.
- ❤ [Fácil de usar] Simplemente coloque la herramienta de medición de ángulo en su área de trabajo, deslice la herramienta de medición de ángulo en la forma deseada y apriete los tornillos. La regla multiángulo se puede colocar en cualquier posición y fijar en cuestión de segundos para crear su propia plantilla. Además, los tornillos incluidos son grandes y se pueden reemplazar con una mano, lo que lo hace muy fácil de usar.
- ❤ [Amplia aplicación] La regla multiángulo de 6 lados es una herramienta universal de medición multiángulo que suministra artículos de ladrillo, madera, baldosas, pisos, techos y metal. Puede elegir un cuadrado de metal como regalo para constructores, solteros, carpinteros, artesanos, techadores, carpinteros, arquitectos, bricolaje, etc.


Silverline - Regla transportador de ángulos 600 mm (783421)
- Regla plegable y transportador de ángulos de acero inoxidable y agujeros para colgar
- Graduaciones métricas e imperiales
- Mide longitud y ángulos
- Buscador de ángulos y tornillo de sujeción
- Ajustable en 360°, precisión +/- 1°


WORKPRO Escuadra Combinada Ajustable Regla de Ángulo de Acero Inoxidable de 300 mm Cuadrado de Combinación con Nivel de Burbuja Recto Escuadra para Carpintería Herramienta de Medición Multifuncional
- 【Material Superior】 La escuadra combinada ajustable es resistente y duradera. La regla está hecha de acero inoxidable de alta calidad y el soporte en ángulo está hecho de aleación de zinc, lo que garantiza que no se oxidará, deformará o romperá fácilmente.
- 【Alta Precisión】 El rango de medición es de 0-300 mm, regla de doble cara en graduaciones métricas y en pulgadas para una lectura fácil y precisa. Al mismo tiempo, combina una burbuja de nivel, mide con precisión el equilibrio para mejorar la eficiencia del trabajo.
- 【Medición Multifuncional】 Esta regla de ángulo puede medir una variedad de datos, como ángulo recto, ángulo de 45 °, longitud, profundidad y anchura.
- 【Diseño Ajustable】 El tornillo de resorte y el sistema de sujeción eficiente facilitan la extracción e instalación de la regla de acero inoxidable, y la regla suave también facilita la medición deslizante.
- 【Aplicación Amplia】 Esta escuadra combinada es adecuada para medir, marcar, etc., para ayudarlo a medir con precisión. Es ampliamente utilizado en el hogar, medición de ingeniería, construcción de viviendas y otros lugares.


Transportadores de Ángulos Digital,Preciva Medidor de angulos digital,Regla Angulos Acero Inoxidable,medidor angulos,medición de 0-400 mm y 360° Ángulo de Medición
- ♚Transportador digital 2 en 1 La regla digital de acero inoxidable y el buscador de ángulos hacen mediciones precisas. El mecanismo de bisagra en la regla de ángulo permite una medición completa de 360 grados de ángulos internos e inversos; El transportador combina escalas de escala estándar y métricas. Medición de ángulos relativos y absolutos.
- ♚Transportador de buscador de ángulo digital, Transportador digital Preciva Regla de medición de acero inoxidable de 7 pulgadas / 400 mm con pantalla LCD grande para carpintería, medición, herramienta de medición de ángulo de construcción
- ♚Reglas duraderas y bajo consumo de energía El medidor de ángulo del transportador digital y el cuerpo de acero inoxidable duradero del buscador de ángulo se pueden utilizar durante mucho tiempo; Función HOLD y RESET, escala de grabado láser, clara y precisa, no se caerá. Además, también tiene la ventaja de ahorrar energía, se cerrará automáticamente después de 6 minutos de inactividad.
- ♚Batería incluida Gran capacidad en espera con función de apagado automático, utiliza una batería de botón CR2032 para trabajar durante más de 2000 horas. Ahorra consumo de energía y prolonga la vida útil de la batería.
- ♚

Ángulo Escuadra Grado

goobay Cable de red 51536 CAT 6A, 90 grados, Ethernet, Playstation, Xbox, LAN, DSL, U/UTP, RJ45, color blanco, 1 m
- Cable de red LAN/adecuado para redes Gigabit 10/100/1000/10000 Mbit, ancho de banda máximo 500 MHz, adecuado para alimentación a través de Ethernet (PoE/PoE+)
- Conector RJ45 recto en ángulo RJ45, solución ideal en espacios mínimos, protección de la nariz e indicación de longitud en el conector recto
- Cable redondo de revestimiento de PVC, conductor interior de aluminio revestido de cobre, protección contra torceduras en ambos lados
- Ideal para consolas con imágenes de alta resolución como, por ejemplo, PS 4, PS 5, Xbox One, Xbox One X, Nintendo, etc.
- Compatible con cables CAT 5


50 Piezas Soportes de Esquina para Conectores Angulares Soporte de Esquina 90 Grados de Acero Inoxidable Grado Soporte de Angulo Escuadras Angulos Metalicos 20 X 20 mm Escuadras para Estanterias
- 【Contenido del Paquete】Obtendrá 50pcs escuadra metalica + 100pcs tornillos, tamaño 20*20*16 mm/0.78*0.78*0.62in.Diámetro del agujero: 5 mm.Soporte angular de acero en forma de L, refuerzo ideal para uso a largo plazo!
- 【Duradero】Nuestros conectores de angulo están hechos de acero inoxidable de alta calidad, a prueba de óxido y resistente, con tratamiento de superficie cepillada, lisa y sin rebabas. Fuerte capacidad de carga, no es fácil de deformar, equipado con tornillos de montaje. El ángulo es de 90°, moldeado en una sola pieza para garantizar una gran capacidad de carga. Fácil de usar.
- 【Gran Capacidad de Carga】Nuestro ángulo de acero inoxidable en forma de L está diseñado con 90°, fundición a presión de acero sólido, Soporte de angulo de acero inoxidable en forma de L con tornillos alta dureza y fuerte capacidad de carga para garantizar la estabilidad y fiabilidad del soporte.
- 【Fácil de Instalar】Nuestros soportes de acero inoxidable están diseñados con tornillos avellanados que no sobresalen, manteniendo el aspecto de sus muebles. Primero taladre los agujeros, luego instale los tornillos y apriételos. Le permite instalar los soportes de acero rápida y fácilmente. Soporte de fijación en angulo recto soporte de angulo en forma de L son ideales para el bricolaje!
- 【Amplio Uso】Las escuadras metálicas en forma de L son adecuadas para bricolaje en madera, estanterías, mesas, sillas, armarios, cómodas, camas, construcción de marcos de madera y cajas, etc . Para estabilidad y refuerzo. Los soportes angulares de acero inoxidable también se pueden utilizar como estantes de almacenamiento para aumentar el espacio de almacenamiento y mejorar las opciones de almacenamiento.

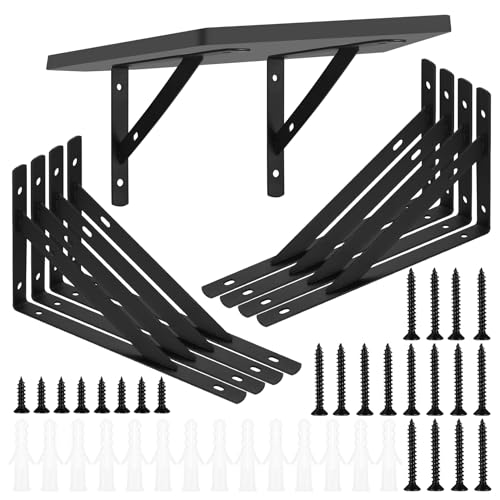
8 Piezas Soportes para Estantes de Pared, Escuadra para Estanterías, Soportes Estantes Triangulares de 90 Grados Angular de Montaje en Pared Pesados para Cocina Libros Estante, 200x120 mm
- Material premium: los escuadras soportes para estantes de pared están hechos de material de hierro sólido con una estructura triangular resistente, que es resistente, resistente al desgaste, resistente a la corrosión, resistente al óxido y duradero.
- Diseño triangular: el diseño de escuadras ángulo recto de 90 grados tiene una estructura triangular fuerte que proporciona una gran estabilidad y capacidad de carga. El diseño de filete y el borde liso aumentan la seguridad y lo protegen de los rasguños.
- Fácil de instalar: el paquete viene con todo el hardware que necesita, incluye soportes para estantes y todos los tornillos y anclajes. Solo necesita preparar un destornillador para instalarlo fácilmente.
- Amplias aplicaciones: estos soportes escuadra estanteria para estantes montados en la pared se pueden usar para estanterías, estantes de jardín, esquinas de mesas y sillas, etc. Ideal para cocina, baño, dormitorio, oficina y más.
- El paquete incluye: Recibirá 8 soportes para estantes resistentes, 16 anclajes de plástico para paneles de yeso (28 mm/1,10"), 16 tornillos largos (30 mm/1,2"), 16 tornillos cortos (16 mm/0,63"). Servicio de aduanas). Ahorre espacio y mantenga la habitación ordenada.


24 Piezas Angulos Metalicos con 100 Tornillos, 30×30×16mm Conectores en ángulo, 90 Grados Escuadras Metalicas, Soporte de Esquina Acero Inoxidable, Soportes en Forma L Negros para Mesa, Armario, Silla
- ✅【Materiales de Calidad】El soporte de esquina de metal está hecho de acero inoxidable de alta calidad, la superficie está tratada con pintura negra y los bordes están libres de rebabas. No es fácil de oxidar, sólido y duradero, adecuado para uso a largo plazo en interiores y exteriores, hermoso y práctico, agujeros avellanados para garantizar que los tornillos no sobresalgan, haciendo que sus muebles sean hermosos y generosos.
- ✅【Fácil de Instalar】 Soporte de metal de ángulo recto de 90 grados con diseño en forma de L, el soporte de esquina tiene una estructura simple para asegurar que las partes de los muebles sean firmes y estables, el juego viene con tornillos para una fácil instalación. Solo necesita perforar agujeros, instalar los tornillos y apretarlos con un destornillador, adecuado para estabilizar puertas de madera, marcos de cama, cofres, muebles, puertas de armarios, cómodas y así sucesivamente.
- ✅【Gran Capacidad de Carga】La parte media del soporte tiene un diseño especial de esquina reforzada, la ranura media duplica la capacidad de carga del soporte, moldeado de una sola pieza, estabilidad estructural, capaz de encajar estrechamente con los muebles, y el montaje 4 Los agujeros de los tornillos se distribuyen uniformemente, no es fácil dañar los objetos, y efectivamente proporcionar un mejor soporte.
- ✅【Amplias Aplicaciones】Como conector de esquina, el soporte es muy conveniente para fijar y reparar todo tipo de muebles de madera (mesas, sillas, armarios, estanterías, camas, armarios, armarios, puertas y ventanas, etc.). Además, también se utiliza mucho en exteriores (vallas, cobertizos, cuartos de mascotas, cuartos de herramientas)
- ✅ 【Contenido del Paquete】Hay un total de 24pcs soportes de acero inoxidable en forma de L y 100pcs 3,5 x16mm tornillos en el set.El espesor de los soportes de acero inoxidable en forma de L es de 1,8 mm, Tamaño: 30 x 30 x 16 mm, Diámetro del agujero: 5 mm.Cantidad suficiente para satisfacer sus necesidades diarias para una amplia gama de muebles y hardware.

