¿Cuáles son los divisores de 108?

108 es un número entero que tiene varios divisores. Un divisor es un número que se divide exactamente en otro número sin dejar residuo. Para encontrar los divisores de 108, podemos comenzar dividiendo 108 por 2. Si la división es exacta, entonces 2 es un divisor de 108.

Al dividir 108 por 2, obtenemos 54. Esto significa que 2 es un divisor de 108. Ahora, vamos a dividir 108 por 3.

Al dividir 108 por 3, obtenemos 36. Esto significa que 3 es un divisor de 108. Podemos continuar dividiendo 108 por 4, 5, 6, y así sucesivamente.

Al dividir 108 por 4, obtenemos 27. Esto significa que 4 es un divisor de 108. Al dividir 108 por 5, obtenemos un resultado decimal, lo que indica que 5 no es divisor de 108.

Continuando con esta metodología, encontramos que los otros divisores de 108 son 6, 9, 12, 18, 27, 36 y 54. En total, 108 tiene 9 divisores.

En conclusión, los divisores de 108 son 2, 3, 4, 6, 9, 12, 18, 27, 36 y 54. Estos números se dividen exactamente en 108 sin dejar residuo.

¿Cuáles son los divisores de 180?

¿Cuáles son los divisores de 100?

Los divisores de 100 son los números que pueden dividir a 100 exactamente sin dejar residuo. En este caso, los divisores de 100 son 1, 2, 4, 5, 10, 20, 25, 50 y 100.

El número 100 se puede dividir por 1 ya que todo número es divisible por 1. De igual manera, el número 100 se puede dividir por sí mismo, es decir, por 100. Estos dos números siempre serán divisores de cualquier número.

Además de estos dos divisores, el número 100 se puede dividir por otros números. Por ejemplo, el 100 se puede dividir por 2 ya que 100 dividido por 2 es igual a 50. De igual manera, el 100 se puede dividir por 4 ya que 100 dividido por 4 es igual a 25.

Otro divisor del 100 es el número 5. Si dividimos 100 entre 5, obtenemos como resultado 20. También se puede dividir por 10, ya que 100 dividido por 10 es igual a 10.

Además, el número 100 puede ser dividido por 20, ya que al dividirlo entre 20 obtenemos como resultado 5. De la misma manera, el 100 se puede dividir por 25, ya que 100 dividido por 25 es igual a 4.

Finalmente, el número 100 también puede ser dividido por 50, ya que 100 dividido por 50 es igual a 2.

En resumen, los divisores de 100 son 1, 2, 4, 5, 10, 20, 25, 50 y 100.

¿Cuáles son los divisores de 126?

Los divisores de 126 son los números enteros que pueden dividir a 126 sin dejar residuo. Estos números son importantes para conocer las distintas combinaciones posibles de descomponer a 126 en factores. Para determinar los divisores de un número, se pueden realizar diversas estrategias.

En primer lugar, es importante mencionar que el número 126 es un número compuesto, es decir, no es un número primo. Esto significa que tiene más de dos divisores. Los divisores de un número compuesto se obtienen a partir de su factorización.

Para factorizar a 126, se puede comenzar por descomponerlo en factores primos. Observamos que 126 es divisible por 2 ya que es un número par, por lo que podemos dividirlo entre 2 y obtenemos 63. Luego continuamos dividiendo entre 3 hasta obtener el número primo 7. Por lo tanto, la factorización de 126 es 2 x 3 x 3 x 7.

Para determinar los divisores de 126, podemos combinar los factores primos de manera que se obtengan diferentes multiplicaciones de ellos. Al hacer esto, obtenemos los siguientes divisores: 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63 y 126. Estos son los números enteros que pueden dividir a 126 sin dejar residuo.

Es importante tener en cuenta que 1 y el propio número, en este caso 126, son siempre divisores de cualquier número entero. Además, es posible notar que los divisores de un número están en una relación inversa entre sí. Esto significa que si un número es divisor de otro, su cociente también será divisor.

Conocer los divisores de un número como 126 es útil en matemáticas para trabajar con fracciones, simplificar expresiones algebraicas o calcular el Mínimo Común Múltiplo (MCM) y el Máximo Común Divisor (MCD) de distintos números. Además, permite identificar cuáles son los números que cumplan una condición particular, como números pares, números impares o números primos.

En conclusión, los divisores de 126 son 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63 y 126. Estos números son importantes para analizar las diferentes propiedades y características del número 126, así como para realizar operaciones matemáticas y simplificaciones algebraicas.

¿Cómo se calcula la cantidad de divisores de un número?

Calcular la cantidad de divisores de un número es un proceso matemático que puede llevarse a cabo de diferentes formas. Una de las estrategias más comunes es realizar la factorización del número en cuestión. Para ello, se descomponen sus factores primos y se obtiene su representación en términos de potencias de primos.

Una vez que se ha factorizado el número, el siguiente paso consiste en aplicar la fórmula que permite determinar la cantidad de divisores. Esta fórmula establece que, si un número se expresa como el producto de factores primos elevados a diferentes potencias, la cantidad de divisores es igual al producto de las potencias incrementado en uno en cada caso. Es decir, si un número se representa como p1^e1 * p2^e2 * p3^e3 * ... * pn^en, donde p1, p2, p3, ..., pn son números primos distintos y e1, e2, e3, ..., en son las respectivas potencias, entonces la cantidad de divisores del número será (e1 + 1) * (e2 + 1) * (e3 + 1) * ... * (en + 1).

Por ejemplo, si queremos calcular la cantidad de divisores del número 24, primero debemos factorizarlo en términos de factores primos: 24 = 2^3 * 3^1. A partir de esta factorización, podemos aplicar la fórmula para obtener el resultado. En este caso, la cantidad de divisores de 24 será (3 + 1) * (1 + 1) = 4 * 2 = 8.

Es importante destacar que esta fórmula es válida únicamente para números enteros positivos. En caso de que el número en cuestión sea negativo, es necesario tomar su valor absoluto antes de proceder con la factorización y el cálculo de la cantidad de divisores.

Divisor

vidaXL Biombo Divisor de 6 Paneles Separador Decoración Habitación Dormitorio Oficina Pantalla Privacidad Pared Plegable de Tela Gris Antracita

• Función versátil: No solo puedes utilizar el biombo para separar el dormitorio y el salón o para bloquear una zona de la estancia si lo necesitas, sino que también puedes colocarlo al lado de la ventana para bloquear la luz del sol. Por supuesto, incluso puedes usar el biombo como pared de fondo.
• Material duradero: La tela posee un aspecto sencillo y limpio, y es transpirable y duradera.
• Función versátil: No solo puedes utilizar el biombo para separar el dormitorio y el salón o para bloquear una zona de la estancia si lo necesitas, sino que también puedes colocarlo al lado de la ventana para bloquear la luz del sol. Por supuesto, incluso puedes usar el biombo como pared de fondo.
• Diseño plegable: Este biombo de 6 paneles es plegable, por lo que puedes guardarlo fácilmente sin que ocupe demasiado espacio.
• Color: Gris antracita;Material: Tela (100% poliéster), hierro;Dimensiones totales: 300 x 200 cm (ancho x alto)

Ver precios en

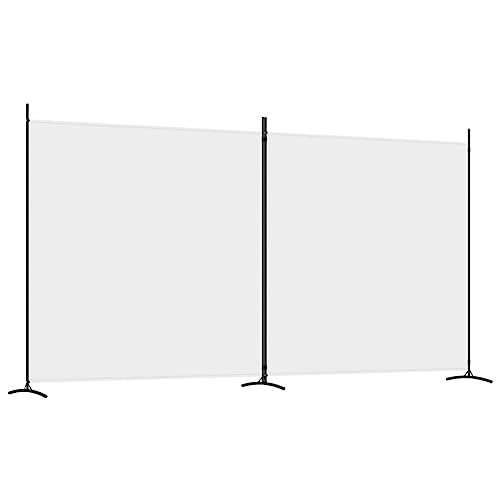
vidaXL Biombo Divisor de 2 Paneles Separador Decoración Habitación Dormitorio Oficina Pantalla Privacidad Pared Plegable de Tela Blanco

• Este biombo puede dividir una estancia en varias partes para proporcionar un espacio privado y proteger tu intimidad.
• Material duradero: La tela posee un aspecto sencillo y limpio, y es transpirable y duradera.
• Función versátil: No solo puedes utilizar el biombo para separar el dormitorio y el salón o para bloquear una zona de la estancia si lo necesitas, sino que también puedes colocarlo al lado de la ventana para bloquear la luz del sol. Por supuesto, incluso puedes usar el biombo como pared de fondo.
• Diseño plegable: Este biombo de 2 paneles es plegable, por lo que puedes guardarlo fácilmente sin que ocupe demasiado espacio.
• Color: Blanco;Material: Tela (100% poliéster), hierro;Dimensiones totales: 348 x 180 cm (ancho x alto)

Ver precios en

SUCESO Cable Divisor Splitter Jack Auriculares 3,5mm Macho a 2 Hembra Cable Nylon Trenzado Audio Estéreo Splitter para Samsung,Huawei,HTC,Sony,LG,Tablet,Auriculares,Altavoz,MP3,Laptop-35cm(Negro)

• Fácil de compartir: Este adaptador divisor de auriculares es la mejor solución para escuchar música juntos con dos auriculares. Este diseño tipo Y le permite compartir su música, películas y juegos favoritos con sus familiares y amigos desde un solo dispositivo.
• Calidad de sonido incomparable: Construido con un conector chapado en oro de doble blindaje y un núcleo de alambre de cobre y oxígeno que lo hace menos susceptible a la interferencia externa, ofrece un sonido estéreo claro y limpio en ambas salidas.
• Compatibilidad universal: adaptador jack 3.5mm macho a 2 hembras está diseñado para compartir audio.- sirve para cualquier dispositivo portátil que utilice un jack de 3.5mm.tales como iPad, iPhone, iPod, reproductor de MP3, computadora portátil, PC, teléfono móvil, tableta u otros dispositivos de audio con un conector para auriculares de 3.5 mm.
• Durabilidad sobresaliente: Los contactos chapados en oro de 24K son a prueba de herrumbre y más duraderos al enchufar y desenchufar el cable. La vida útil de curvatura de más de 15000 y el exterior de nylon trenzado doble hacen que el divisor de auriculares se agregue a la durabilidad y sin enredos
• Lo que obtiene: puede obtener Cable Divisor Splitter Jack Auriculares 3,5mm. Si tiene alguna pregunta sobre el producto, no dude en contactarnos.

Ver precios en

vidaXL Biombo Divisor Bambú Natural 250x165 cm Separador Habitación Privacidad

• El divisor es completamente opaco, ofreciendo privacidad completa
• Será un aporte práctico y decorativo a su dormitorio, sala de estar u oficina.El divisor de habitación está hecho de bambú, que es robusto y duradero y aportará un toque natural a su interior
• El divisor es completamente opaco, ofreciendo privacidad completa
• Se puede enrollar fácilmente cuando no se use para transportarlo y almacenarlo fácilmente
• La pantalla de privacidad de bambú se puede poner en distintas configuraciones gracias a su flexibilidad

Ver precios en

divisores de 803

Naber STOREX 803.4.065 - Divisor para cajones (3 unidades), color blanco translúcido

• 3 unidades. Color blanco translúcido.

Ver precios en

goCoax Adaptador Moca 2.5 con Puerto Ethernet de 2.5 GbE. Moca 2.5. 1x 2.5 GbE. Proporcionar Ancho de Banda de 2.5 Gbps con Cables coaxiales existentes. Blanco (Paquete único, MA2500D)..

• MoCA 2.5 can offer extremely high bandwidth of 2.5 Gbps. This bandwidth are shared by all the MoCA devices in the same coaxial network. That’s more than enough to allow streaming 4K/8K videos at the same time, while still playing an online game and transferring pictures from a computer or a mobile device to a television for viewing.
• Combined with the 2.5GbE Ethernet inerface, our product can provide the real 2.5Gbps backhual to your home network. This is a cost effective and amazing upgrading.
• Unlike Wi-Fi, MoCA is based on coaxial cable, a shielded metal wire. That can minimize the external interference. Also the attenuation of the cable is very small, less than 8dB per 100 feet. Even with a 60dB path loss, you still can get a full-speed connection. It is almost comparable to Ethernet.
• Improve online gaming by lower latency. Latency is the important quality of your network, it is the term used to indicate any kind of delay that happens in data communication over a network. When play games online, latency is critical. The lower latency, the better gaming experience. MoCA 2.5 can achieve 3ms delay. For Wi-Fi, the value is variable, from milliseconds to tens of milliseconds. So MoCA is the best choice for gaming players.
• Please buy at least two devices to enjoy the high speed MoCA 2.5. They can be connected to a variety of devices in the home. Maximum 16 MoCA devices in every home network.

Ver precios en

AIHOUSE Bloque de distribución de energía 0 Calibre en 4 maniombrador de 2 vías Distribución de Bloque de Cobre de Cobre para el Divisor de Audio de Coche

• Bloque de distribución de audio de cobre de cobre de alto rendimiento de cobre sólido.
• Construcción sólida Durable Base de alta temperatura y alojamiento resistente al calor claro.
• 1-0 / 2/4 GAUGE AWG IN, 2-4 / 6/8 GAUGE AWG OUT, Fácil instalación para combinaciones de múltiples.
• Diseño de ahorro de espacio compacto, mini tamaño pero alto acabado de conductividad.
• Aplicable a automóviles, embarcaciones u otros vehículos, proteja su sistema de audio.

Ver precios en

Estante divisor de archivos, organizador de archivos de escritorio de alambre vertical de 3 ranuras Organizador de escritorio de cuero sintético multifuncional, para el hogar de la oficina,Marrón

• Multifunción: revistero ideal para el almacenamiento de todos sus artículos de oficina, como papel A4, documentos, cuadernos, bolígrafos y otras cosas pequeñas. Este porta archivo de revista es la mejor opción para hacer que su escritorio esté en orden. Puedes usarlo en tu oficina, en la escuela, en casa, casi en todas partes.
• Diseño: con una perspectiva única, y tiene 3 compartimentos donde puede clasificar sus cosas según su preferencia. Es el mejor divisor de archivos.
• Montaje rápido y fácil: este estante de archivos es portátil y fácil de ensamblar, solo 5 a 10 minutos para terminar el ensamblaje sin herramientas, lo que ahorra bastante tiempo y es conveniente.
• Material: este clasificador de revistas está hecho de cuero de madera, con una construcción sólida y de alta calidad, no es frágil ni susceptible de doblarse o moverse, también es fácil de limpiar y puede proteger del polvo y el agua. Instrucciones de cuidado: fácil de limpiar Solo Limpie con un paño seco.
• DISEÑO: mantenga el desorden de su escritorio libre y ordenado. Cuenta con una unidad de almacenamiento de documentos de nuevo diseño para almacenar sus documentos necesarios. Este organizador de madera puede hacer que incluso el correo basura se vea bien. Colóquelo en el pasillo para guardar cartas, revistas y billetes a medida que ingresan a su hogar. Incluso podría comprar dos y usar uno para guardar cartas para enviar por correo, su billetera y llaves a mano.

Ver precios en