¿Cuáles son los divisores de 11?

11 es un número primo, lo que significa que solo tiene dos divisores: 1 y 11. Los divisores de un número son aquellos números enteros con los que se puede dividir uniformemente. Al ser 11 primo, no puede ser dividido por ningún otro número entero sin dejar un residuo.

El número 1 es un divisor de cualquier número, ya que cualquier número dividido por 1 es igual al número original. En este caso, 11 dividido por 1 es 11.

El número 11 también es un divisor de sí mismo, ya que cualquier número dividido por sí mismo siempre es igual a 1. En este caso, 11 dividido por 11 es 1.

Estos son los únicos dos divisores de 11. No hay otros números enteros que se puedan dividir uniformemente en 11 sin dejar un residuo. Por lo tanto, podemos concluir que los divisores de 11 son 1 y 11.

¿Cuál es el divisor de 12?

El divisor de 12 es un número que puede ser dividido exactamente en 12 partes iguales sin dejar un residuo. Para encontrar el divisor de 12, debemos buscar todos los números enteros que dividan a 12 sin dejar residuo.

En primer lugar, podemos dividir 12 entre 1, y obtenemos como resultado 12. Esto significa que 1 es un divisor de 12.

A continuación, dividimos 12 entre 2, y también obtenemos 6 como resultado. Por lo tanto, 2 es otro divisor de 12.

Seguimos dividiendo 12 entre 3, y el resultado es 4. Así que 3 también es un divisor de 12.

Dividimos 12 entre 4, y obtenemos 3 como resultado. Por lo tanto, 4 también es un divisor de 12.

Luego, dividimos 12 entre 5, pero el resultado es 2.4, lo cual no es un número entero. Por lo tanto, 5 no es un divisor de 12.

Continuando con la búsqueda, dividimos 12 entre 6, y obtenemos 2 como resultado. Por lo tanto, 6 es un divisor de 12.

Dividimos 12 entre 7, pero el resultado es 1.714, nuevamente no es un número entero. Entonces, 7 no es un divisor de 12.

Finalmente, dividimos 12 entre 8, pero obtenemos 1.5, que tampoco es un número entero. Por lo tanto, 8 no es un divisor de 12.

En resumen, los divisores de 12 son 1, 2, 3, 4 y 6, ya que estos números pueden dividir exactamente a 12 sin dejar residuo.

¿Cuál es el divisor de 17?

El número 17 es un número primo, lo que significa que solo tiene dos divisores: el 1 y él mismo. Por lo tanto, el único divisor de 17 es el número 17.

Un número primo es aquel que solo es divisible entre 1 y sí mismo. En el caso del número 17, no existen otros números enteros positivos que lo dividan sin dejar residuo. Es decir, 17 no tiene ningún divisor adicional.

Esto contrasta con los números compuestos, que tienen más de dos divisores. Por ejemplo, el número 12 es divisible por 1, 2, 3, 4, 6 y 12, lo que lo convierte en un número compuesto. Sin embargo, el número 17 no tiene esa característica, siendo un número primo.

Los números primos son fundamentales en matemáticas y tienen propiedades únicas que los distinguen de los números compuestos. Además de su importancia teórica, los números primos también tienen numerosas aplicaciones prácticas en criptografía, algoritmos y otras áreas de la ciencia y la tecnología.

¿Cuál es el divisor de 13?

A lo largo de la historia, los matemáticos han dedicado mucho tiempo y esfuerzo a comprender los números y las propiedades que los rodean. Uno de los conceptos más relevantes en el ámbito de las matemáticas es el de los divisores. Un divisor de un número es aquel número entero que divide a otro número sin dejar residuo.

En el caso particular del número 13, nos preguntamos cuál es su divisor. Para determinar cuáles son los divisores de un número, debemos buscar los números enteros que dividan a 13 sin dejar residuo. En este caso, podemos ver que los números 1 y 13 son divisores de 13. Esto se debe a que 13 dividido entre 1 y 13 da como resultado un cociente entero sin residuos.

Algo interesante sobre el número 13 es que no tiene más divisores. No encontraremos ningún otro número entero distinto de 1 y 13 que divida a 13 sin dejar residuo. Esto se debe a que 13 es un número primo, es decir, solo tiene dos divisores. Los números primos son aquellos que no pueden ser divididos por ningún otro número entero distinto de sí mismos y de 1.

En resumen, el divisor de 13 es el número 1 y el número 13. Estos son los únicos dos números enteros que dividen a 13 sin dejar residuo. Es importante recordar que el número 13 es un número primo, lo cual significa que solo tiene dos divisores. El estudio de los divisores y las propiedades de los números es una parte fundamental de las matemáticas, y comprendiendo estos conceptos podemos entender mejor cómo se relacionan entre sí los números.

¿Cómo saber cuántos divisores tiene un número?

Para saber cuántos divisores tiene un número, debemos entender qué es un divisor. Un divisor es un número que divide exactamente a otro número sin dejar residuo. Por ejemplo, los divisores del número 12 son 1, 2, 3, 4, 6 y 12.

Existen varios métodos para calcular los divisores de un número. Uno de ellos es el método de la factorización. Este método consiste en descomponer el número en sus factores primos y luego contar cuántas combinaciones diferentes se pueden formar con ellos.

Por ejemplo, si queremos saber cuántos divisores tiene el número 24, debemos factorizarlo en sus factores primos, que en este caso son 2, 2 y 3. Luego, contamos todas las combinaciones posibles de estos factores: 2^0 * 3^0, 2^1 * 3^0, 2^2 * 3^0, 2^0 * 3^1, 2^1 * 3^1 y 2^2 * 3^1. Esto nos da un total de 6 combinaciones posibles, por lo que concluimos que el número 24 tiene 6 divisores.

Otro método para calcular los divisores de un número es utilizando su forma binomial elevada a una potencia. Por ejemplo, si tenemos un número de la forma p^a * q^b, donde p y q son primos y a y b son enteros positivos, entonces el número de divisores será (a + 1) * (b + 1).

Por ejemplo, si queremos saber cuántos divisores tiene el número 36, podemos escribirlo como 2^2 * 3^2. Aplicando la fórmula, obtenemos (2 + 1) * (2 + 1) = 3 * 3 = 9. Por lo tanto, concluimos que el número 36 tiene 9 divisores.

En resumen, para saber cuántos divisores tiene un número, podemos utilizar diferentes métodos como la factorización y la fórmula de la forma binomial. Estos métodos nos permiten calcular rápidamente la cantidad de divisores que tiene un número determinado.

Divisor

vidaXL Biombo Divisor de 6 Paneles Separador Decoración Habitación Dormitorio Oficina Pantalla Privacidad Pared Plegable de Tela Gris Antracita

• Función versátil: No solo puedes utilizar el biombo para separar el dormitorio y el salón o para bloquear una zona de la estancia si lo necesitas, sino que también puedes colocarlo al lado de la ventana para bloquear la luz del sol. Por supuesto, incluso puedes usar el biombo como pared de fondo.
• Material duradero: La tela posee un aspecto sencillo y limpio, y es transpirable y duradera.
• Función versátil: No solo puedes utilizar el biombo para separar el dormitorio y el salón o para bloquear una zona de la estancia si lo necesitas, sino que también puedes colocarlo al lado de la ventana para bloquear la luz del sol. Por supuesto, incluso puedes usar el biombo como pared de fondo.
• Diseño plegable: Este biombo de 6 paneles es plegable, por lo que puedes guardarlo fácilmente sin que ocupe demasiado espacio.
• Color: Gris antracita;Material: Tela (100% poliéster), hierro;Dimensiones totales: 300 x 200 cm (ancho x alto)

Ver precios en

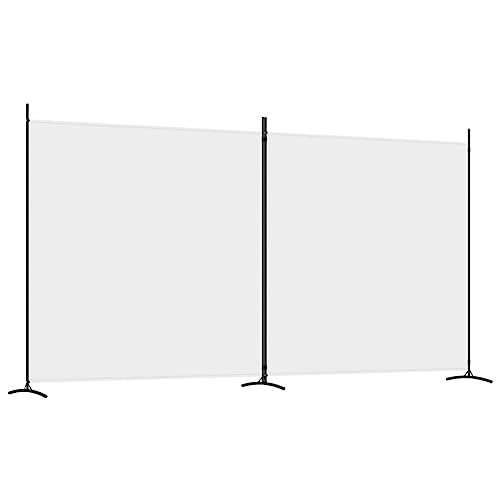
vidaXL Biombo Divisor de 2 Paneles Separador Decoración Habitación Dormitorio Oficina Pantalla Privacidad Pared Plegable de Tela Blanco

• Este biombo puede dividir una estancia en varias partes para proporcionar un espacio privado y proteger tu intimidad.
• Material duradero: La tela posee un aspecto sencillo y limpio, y es transpirable y duradera.
• Función versátil: No solo puedes utilizar el biombo para separar el dormitorio y el salón o para bloquear una zona de la estancia si lo necesitas, sino que también puedes colocarlo al lado de la ventana para bloquear la luz del sol. Por supuesto, incluso puedes usar el biombo como pared de fondo.
• Diseño plegable: Este biombo de 2 paneles es plegable, por lo que puedes guardarlo fácilmente sin que ocupe demasiado espacio.
• Color: Blanco;Material: Tela (100% poliéster), hierro;Dimensiones totales: 348 x 180 cm (ancho x alto)

Ver precios en

SUCESO Cable Divisor Splitter Jack Auriculares 3,5mm Macho a 2 Hembra Cable Nylon Trenzado Audio Estéreo Splitter para Samsung,Huawei,HTC,Sony,LG,Tablet,Auriculares,Altavoz,MP3,Laptop-35cm(Negro)

• Fácil de compartir: Este adaptador divisor de auriculares es la mejor solución para escuchar música juntos con dos auriculares. Este diseño tipo Y le permite compartir su música, películas y juegos favoritos con sus familiares y amigos desde un solo dispositivo.
• Calidad de sonido incomparable: Construido con un conector chapado en oro de doble blindaje y un núcleo de alambre de cobre y oxígeno que lo hace menos susceptible a la interferencia externa, ofrece un sonido estéreo claro y limpio en ambas salidas.
• Compatibilidad universal: adaptador jack 3.5mm macho a 2 hembras está diseñado para compartir audio.- sirve para cualquier dispositivo portátil que utilice un jack de 3.5mm.tales como iPad, iPhone, iPod, reproductor de MP3, computadora portátil, PC, teléfono móvil, tableta u otros dispositivos de audio con un conector para auriculares de 3.5 mm.
• Durabilidad sobresaliente: Los contactos chapados en oro de 24K son a prueba de herrumbre y más duraderos al enchufar y desenchufar el cable. La vida útil de curvatura de más de 15000 y el exterior de nylon trenzado doble hacen que el divisor de auriculares se agregue a la durabilidad y sin enredos
• Lo que obtiene: puede obtener Cable Divisor Splitter Jack Auriculares 3,5mm. Si tiene alguna pregunta sobre el producto, no dude en contactarnos.

Ver precios en

vidaXL Biombo Divisor Bambú Natural 250x165 cm Separador Habitación Privacidad

• El divisor es completamente opaco, ofreciendo privacidad completa
• Será un aporte práctico y decorativo a su dormitorio, sala de estar u oficina.El divisor de habitación está hecho de bambú, que es robusto y duradero y aportará un toque natural a su interior
• El divisor es completamente opaco, ofreciendo privacidad completa
• Se puede enrollar fácilmente cuando no se use para transportarlo y almacenarlo fácilmente
• La pantalla de privacidad de bambú se puede poner en distintas configuraciones gracias a su flexibilidad

Ver precios en

divisores 11

Plus Office - Separadores de Archivador A4 con 12 pestañas de polipropileno 100% reciclable, Números 1-12, Divisores 11 Agujeros y Pestañas para Carpetas de Anillas, para uso escolar y oficina

• ✅   Alta calidad: Los separadores polipropileno de 150 micras archivador 4 anillas están hechos de plástico robusto y resistente a la rotura, que puede reutilizarse en varios proyectos, con una excelente protección y durabilidad, y una larga vida útil. Ideal para el uso frecuente en oficinas y escuelas
• ✅  12 separadores numéricos: El paquete incluye 12 separador archivador enumerados del 1 al 12. Todos los colores son elegantes y generosos para ayudarle a distinguir los documentos rápidamente. Ideal para aulas, presentaciones y entornos empresariales, aportando nueva energía y optimismo a su vida
• ✅  Información sobre el tamaño: Nuestros separadores para carpetas vienen con un diseño de 11 agujeros que se adapta a la mayoría de las carpetas de hojas sueltas. Tienen un tamaño universal A4. El material de polipropileno, resistente al agua y a las roturas, se extiende más allá de la página. Mejor protección para sus documentos
• ✅  Amplia aplicación: Los separadores archivador plástico separan la información en informes, manuales, presentaciones, investigaciones, etc., pero también juegan un buen papel en la protección de archivos. Nuestros separadores de pestañas son muy adecuados para el hogar, la escuela o el lugar de trabajo, ya sea un profesional o un estudiante, pueden ayudarle a clasificar y organizar varios trabajos o arreglos. Con pestañas laterales en las que se puede escribir sobre el material para una máxima organización y personalización
• ✅  Regalo práctico: Nuestros separadores de archivos son un regalo práctico para oficinistas, estudiantes y profesores. Ayuda a mantener las notas organizadas y a separar las diferentes secciones, y es igualmente conveniente para los oficinistas, estudiantes o aquellos que necesitan organizar sus archivos personales

Ver precios en

11. División: divisor de dos cifras (Cuadernos calculo) - 9788466713467

• 11. División: Divisor De Dos Cifras
• Tapa blanda
• Español

Ver precios en

Derwent Divisor Proporcional, 11 orificios de Graduación, Para Medir y Dibujar a Escala, Negro, Calidad Profesional, 2300580

• Divisor proporcional para transferir medidas a tus obras de arte, perfecto para artistas profesionales y principiantes de todas las edades, así como estudiantes
• Herramienta indispensable para cualquier artista: use el divisor proporcional para transferir medidas de la vida real y fotos a tus bocetos y obras de arte para conseguir unas proporciones precisas
• Consigue la máxima precisión con esta herramienta de dibujo, escalando tus imágenes en proporciones de 4: 1 a 1: 4 gracias a los 11 agujeros de graduación
• Ahorra espacio gracias a su cómodo sistema de plegado; cabe dentro de nuestro estuche enrollable Derwent Pencil Wrap (0700434)
• Incluye: 1 x Divisor Proporcional de Derwent, 11 Orificios, Color: Negro

Ver precios en

Pacrate Cascos Gaming para PS4/PS5/Xbox One/Nintendo Switch/PC, Auriculares Gaming con Microfono Cascos PS4 con Sonido Envolvente Estéreo, Cascos Gamer con Cancelación de Ruido, Luz LED, Azul

• 🎧Compatibilidad multiplataforma: los cascos gaming Pacrate con micrófono son compatibles con PS4, PS5, PS4 Pro/Slim, PSP, Xbox One, Xbox One X/S, Xbox Series X/S, Nintendo Switch, PC, portátil, iPad y la mayoría. otros dispositivos con conector de audio de 3.5 mm. Tenga en cuenta que la Xbox One original, Xbox 360, iPad Pro y otros dispositivos sin conector de audio de 3.5 mm necesitan un adaptador de Microsoft adicional para ser compatibles. (fuera del alcance de la entrega)
• 🎵Calidad de sonido envolvente estéreo: los Pacrate auriculares gaming están equipados con controladores de audio duales de neodimio de alta densidad de 40 mm, lo que brinda un rendimiento de audio sorprendente. Con graves mejorados, puede disfrutar de una experiencia de juego inmersiva. Los excelentes cascos ps4 son perfectos para una variedad de juegos como tiradores, juegos de carreras, partidos de fútbol y más.
• 🎧Micrófono ajustable con cancelación de ruido: los auriculares con microfono tienen un micrófono ajustable altamente sensible con técnicas de cancelación de ruido para una comunicación eficiente y estable. Filtra la mayor parte del ruido ambiental en su área y permite conversaciones en tiempo real sin demora. El micrófono ajustable de 120° se puede colocar como quieras.
• 👓 Optimizado para una comodidad conveniente: un control deslizante de acero ajustable y buenas almohadillas de proteína transpirable brindan comodidad para esas largas noches de juego. Después de horas de pruebas de uso intensivo, los cascos con microfono permanecen cómodamente en su lugar, incluso después de largos períodos de uso o uso de anteojos. El diseño de copa cerrada de los cascos gamer ayudará a bloquear las distracciones.
• 🎁Los fascinantes cascos nintendo switch crean una atmósfera de juego genial para mejorar la emoción del juego. La interfaz USB se usa únicamente para encender la luz LED. Es una adición genial en escenarios de grabación de video y transmisión en vivo. El mejor regalo de Navidad y cumpleaños para novios, niñas y familiares.

Ver precios en