¿Cuánto es el ángulo de un cuadrado?
El ángulo de un cuadrado es un concepto fundamental en geometría. Un cuadrado es un polígono de cuatro lados iguales y cuatro ángulos rectos.
Los ángulos de un cuadrado son todos iguales y miden 90 grados. Esto significa que cada uno de los cuatro ángulos internos de un cuadrado tiene una medida de 90 grados.
La suma de los ángulos de un cuadrado es de 360 grados. Esto se debe a que cuatro ángulos de 90 grados suman 360 grados en total.
Los ángulos de un cuadrado son ángulos rectos, lo que significa que forman una esquina perfecta de 90 grados. Esta propiedad es una de las características principales que definen a un cuadrado.
Es importante recordar que el ángulo de un cuadrado no cambia, sin importar el tamaño del cuadrado. Ya sea que el cuadrado sea pequeño o grande, los ángulos siempre serán de 90 grados.
En resumen, los ángulos de un cuadrado miden siempre 90 grados y la suma de los ángulos internos es de 360 grados. Esta propiedad es esencial para la definición y la identificación de un cuadrado en la geometría.
¿Cuál es el ángulo de un cuadrado?
El ángulo de un cuadrado es un concepto clave en geometría. Un cuadrado es una figura geométrica de cuatro lados iguales y cuatro ángulos rectos. Este tipo de figura posee propiedades particulares en cuanto a sus ángulos.
Los ángulos de un cuadrado siempre miden 90 grados. Esto significa que cada uno de los cuatro ángulos internos del cuadrado tiene una medida de 90 grados. Tales ángulos son ángulos rectos, lo que implica que forman una línea recta y son perpendiculares entre sí.
La suma de los ángulos internos de un cuadrado siempre es de 360 grados. Esto se debe a que un cuadrado se puede dividir en dos triángulos rectángulos, cada uno con dos ángulos rectos de 90 grados. Al sumar los ángulos de los dos triángulos rectángulos (90 + 90 + 90 + 90), se obtiene la medida total de los ángulos internos del cuadrado.
Es importante tener en cuenta que el ángulo de un cuadrado no depende del tamaño de sus lados, sino de su forma y propiedades geométricas. Esto significa que, sin importar si el cuadrado es grande o pequeño, sus ángulos siempre serán de 90 grados y la suma de los ángulos siempre será 360 grados.
¿Cuántos ángulos de 180 hay en un cuadrado?
Un cuadrado tiene cuatro lados de igual longitud y cuatro ángulos rectos de 90 grados cada uno. Pero ¿cuántos ángulos de 180 hay en un cuadrado?
En realidad, no hay ángulos de 180 grados en un cuadrado. Esto se debe a que la suma de los ángulos internos de un cuadrado siempre es de 360 grados. Es decir, si sumamos los cuatro ángulos de 90 grados, obtendremos un total de 360 grados.
Por lo tanto, los ángulos en un cuadrado son agudos y rectos, pero ninguno alcanza los 180 grados. Esto es lo que hace que un cuadrado sea diferente de un rectángulo o un rombo, donde algunos de los ángulos pueden ser obtusos o incluso llanos, es decir, de 180 grados.
En resumen, un cuadrado tiene cuatro ángulos rectos de 90 grados cada uno, pero ninguno de ellos alcanza los 180 grados. Esto se debe a que la suma de los ángulos internos de un cuadrado siempre es de 360 grados.
¿Cuántos ángulos rectos tiene un cuadrado?
Un cuadrado tiene cuatro ángulos rectos. Esto significa que cada uno de los cuatro ángulos del cuadrado mide exactamente 90 grados. Estos ángulos rectos son una de las características clave que definen a un cuadrado. Además de tener ángulos rectos, un cuadrado también tiene lados iguales, lo que lo convierte en un polígono regular.
La propiedad de tener cuatro ángulos rectos es lo que distingue a un cuadrado de otros polígonos. Otros polígonos, como los triángulos o los rectángulos, también tienen ángulos rectos, pero solo el cuadrado tiene precisamente cuatro de ellos. Los ángulos rectos en un cuadrado son perfectamente perpendiculares entre sí, formando esquinas perfectas.
Los ángulos rectos de un cuadrado son fundamentales para su estructura y simetría. Cada ángulo recto del cuadrado divide los 360 grados de un círculo en cuatro partes iguales, lo que implica que cada ángulo recto tiene una medida de 90 grados. Esta propiedad hace que los ángulos rectos del cuadrado sean únicos y los diferencia de otros polígonos.
En conclusión, un cuadrado tiene cuatro ángulos rectos, lo que significa que cada uno de los ángulos del cuadrado mide exactamente 90 grados. Esta característica es única y fundamental para la definición y estructura del cuadrado. Los ángulos rectos del cuadrado son perfectamente perpendiculares entre sí y dividen el círculo en cuatro partes iguales.
¿Cuántos lados vértices y ángulos tiene un cuadrado?
Un cuadrado es un polígono de 4 lados iguales y 4 ángulos rectos. Además, tiene 4 vértices. Cada uno de estos lados es de igual longitud, lo que hace que todos los ángulos internos sean de 90 grados. Estas características geométricas le proporcionan al cuadrado una serie de propiedades y simetrías que lo distinguen de otros polígonos regulares.
La propiedad más destacada del cuadrado es su simetría bilateral. Esto significa que se puede dividir en dos partes iguales a través de un eje imaginario llamado eje de simetría. Cada una de estas partes refleja exactamente a la otra, por lo que se dice que el cuadrado es simétrico respecto a su eje.
En cuanto a sus lados, el cuadrado se caracteriza por tener cuatro segmentos de igual longitud. Esto implica que se puede construir un cuadrado a partir de un solo lado y sus ángulos rectos asociados. Cada lado se encuentra adyacente a otros dos lados y también comparte un vértice con ellos. Además, cada lado es paralelo a otro y forma ángulos de 90 grados con los lados adyacentes.
En relación a sus vértices, el cuadrado tiene cuatro puntos de intersección donde se encuentran los lados. Estos puntos se conocen como vértices. Cada vértice es común a dos lados adyacentes y comparte un ángulo recto con ellos. Los vértices son puntos importantes en la definición del cuadrado, ya que son esenciales para establecer la forma y la estructura del polígono.
Finalmente, en cuanto a sus ángulos, el cuadrado posee cuatro ángulos internos rectos. Esto significa que cada ángulo mide exactamente 90 grados. Estos ángulos están formados por dos lados adyacentes y se encuentran en cada vértice del cuadrado.
En resumen, un cuadrado tiene 4 lados, 4 vértices y 4 ángulos rectos. Estas propiedades geométricas constituyen las características principales de este polígono regular, lo que lo convierte en una figura única y especial dentro de la geometría.
angulo de un cuadrado

TRANSPORTADOR NAUTICO CUADRADO SIN HILO MC-165 JUNIOR


Fippy Cuadrados de posicionamiento de 90 grados de ángulo recto de 140 x 140 mm, 2 cuadrados de posicionamiento de aleación de aluminio, abrazadera de esquina de 90 grados para carpintería, marco
- Herramientas cuadradas de posicionamiento profesionales: las abrazaderas cuadradas de posicionamiento de aluminio están diseñadas para ayudar a sostener las juntas firmemente y de forma cuadrada a 90 grados exactos. Las abrazaderas de carpintería son adecuadas para trabajos de soldadura de madera, soldadura de ángulo recto de metal y mucho más. La abrazadera de ángulo recto es una herramienta muy práctica que puede hacer que tus proyectos de carpintería sean más fáciles.
- Material de alta calidad: el kit de cuadrados de posicionamiento de 90 grados está hecho de aleación de aluminio de alta calidad y acero inoxidable, superficie roja anodizada, a prueba de óxido, resistente a la corrosión y de larga duración.
- Diseño altamente preciso: esta abrazadera de esquina cuadrada de posicionamiento está disponible en unidades de medición métricas e imperiales (escala de 5.5 pulgadas y escala de 5.5 pulgadas). Con bordes biselados y ángulos perfectos de 90°, se puede utilizar con accesorios para comprobar el posicionamiento de ángulos, el encolado de tableros de madera o soldadura en ángulo recto.
- Amplia aplicación: las abrazaderas de fijación de ángulo recto cuadradas de posicionamiento de 90 grados son ampliamente utilizadas para trabajos de carpintería, como cajas de montaje y bricolaje, cajones, armarios, marcos, armarios de muebles, etc. Al mismo tiempo, estos cuadrados de posicionamiento de carpintería tienen una escala precisa y se pueden utilizar como regla. Es una herramienta ideal para organizar armarios de estantes y mantenerlos cuadrados al montar marcos, armarios o casi cualquier caja.
- Fácil de usar: solo tienes que poner los cuadrados de posicionamiento en la esquina de las piezas y fijarlos con un juego de abrazaderas de madera. Es fácil de usar y mantener las piezas juntas creando un ángulo perfecto de 90 grados. Como tener manos adicionales, muy simple, aumenta en gran medida tu capacidad para hacer esquinas reales de 90 grados.


El Boxer Ideal: Dos cubos, dos ángulos y un cuadrado

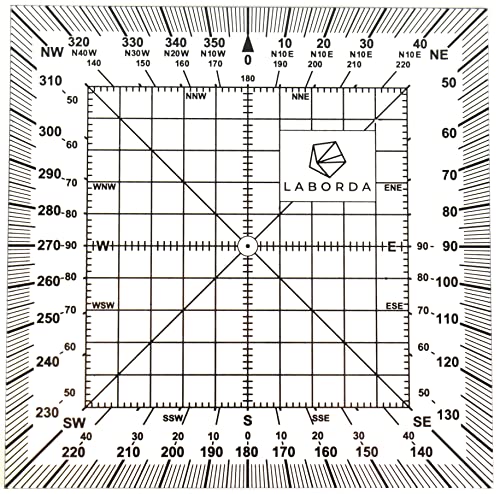
Laborda Transportador de Ángulos Náutico Cuadrado 150 x 150 mm - Fabricado en España
- ALTA CALIDAD: Transportador de óptima densidad y grosor. Posee film protector de PVC garantizando su resguardo. Fabricación 100% en España.
- UTILIDAD: Material imprescindible para resolver los problemas de navegación de manera gráfica en las titulaciones PER y Patrón de Yate.
- CARACTERÍSTICAS: Contiene los rumbos y demoras directos e inversos a lo largo de 360 grados, así como rotulación de los cuadrantales.
- TRABAJAMOS PARA TI: La completa satisfacción de nuestros clientes es nuestra prioridad principal. Nuestro equipo de diseño está enfocado únicamente en crear productos que te sean útiles en tu día a día.

45 Grados

TITA-DONG Máquina biseladora de azulejos,cortador manual de azulejos de 45 grados,aleación de aluminio,porcelana,cerámica,máquina de corte de azulejos de piso de 115-125 mm para amoladora angular de
- Alta precisión: Esta máquina biseladora de azulejos puede cortar chaflanes biselados estándar de 45 grados con alta eficiencia, precisión y simplicidad.
- Diseño fácil de usar: nuestra máquina biseladora de azulejos no solo es fácil de usar, sino que su tamaño compacto la hace altamente portátil. Está diseñado para ser duradero, práctico y ahorra tiempo.
- Corte superior: experimenta una superficie de corte más plana. Nuestra máquina biseladora de azulejos mantiene un contacto cercano con la superficie de corte para cortes suaves y más estables, prometiendo alta resistencia y excelente plasticidad.
- Material de aluminio: la máquina biseladora de azulejos está hecha de aleación de aluminio confiable, que es fuerte y duradera. El trabajo de alta resistencia también mantiene la integridad general y es menos propenso a agrietarse.
- Amplia aplicación: esta máquina biseladora de azulejos puede cortar baldosas, como mármol de cerámica, y también se puede utilizar para cortar piedra y procesar esquinas expuestas, lo que es muy práctico.


Soporte de Esquina de 45 Grados Soporte de Esquina de Aluminio Soporte de Esquina de 6pz para Perfiles de Aluminio 2020 Esquina de Perfil de Aluminio (2020 45 Grados)
- MATERIAL: Escuadra de perfil de aluminio fabricada en aleación de aluminio de alta calidad. Duradero en uso y larga vida útil.
- ACCESORIOS COMPLETOS: 6 escuadras de aluminio + 12 tornillos con hexágono interior + 12 tuercas deslizantes M5 + 12 juntas M5 + 1 llave de 4 mm.
- EXTREMADAMENTE ESTABLE: Estos soportes de esquina fabricados con perfil de aluminio 2020 tienen 2 orificios de fijación. El ángulo de 45 grados mejora el apoyo del punto que conecta el contorno. ¡Bien hecho y muy estable!
- FÁCIL DE USAR: solo use pernos y tuercas para unirlos a los marcos de aluminio. Sencillo, fácil y rápido. ideal para los aficionados al bricolaje que trabajan con perfiles de aluminio.
- MULTIFUNCIONAL: Ampliamente utilizado para la construcción de estructuras industriales de aluminio, impresoras 3D, enrutadores CNC, cortadores láser CNC, barras de luz LED, proyectos de robótica.


AUTOZOCO Adaptador Extensor Valvula neumatico,Adaptador de Válvula Angular, Adaptador de válvula de Cobre, Apto para para Coche, Camión, Bicicletas, Motos y Scooter, 45 Grados
- USO: Este adaptador se conecta a la válvula de inflado del neumático y permite una conexión curva de 45 grados en lugar de una conexión recta. Esto significa que se puede acceder a la válvula de inflado en un ángulo diferente, lo que es útil en situaciones en las que no hay suficiente espacio para conectar una manguera de inflado de neumáticos recta.
- PROTEGE LA VALVULA: Además, el adaptador extensor de válvula neumático curva de 45 grados también puede reducir el estrés y la tensión en la válvula de inflado del neumático, lo que puede prolongar su vida útil y prevenir posibles daños a la válvula. En general, este accesorio es muy útil para facilitar la tarea de inflar neumáticos en espacios reducidos o de difícil acceso, y para proteger la válvula de inflado del neumático.
- APTO PARA para Coche, Camión, Bicicletas, Motos y Scooter
- [ Servicio de atención al cliente ] Si tiene algún problema con el artículo, póngase en contacto con nosotros por correo electrónico, haremos todo lo posible para responderle dentro de las 24 horas.


Donnagelia 45 grados 4 ranuras de ángulo de desplazamiento de montaje de riel Picatinny & Weaver estilo para el montaje de la linterna de punto rojo
- Desplazamiento de 45 grados: sin interferencias en los agarres verticales, protectores de manos u ópticas. Permite un fácil acceso para encender/apagar tu linterna, mira de puntos rojos, etc.
- Material: aluminio de alta calidad con excelente artesanía, resistente, resistente a la corrosión y duradero.
- Diseño ergonómico para una fácil instalación y uso.
- Ideal para rieles de estilo tejedor/picatinny. Una buena idea para montar las miras reflectantes de respaldo junto con tu óptica primaria.
- Mejora tu experiencia de disparo.

