¿Qué medidas se toman para sacar una escuadra?

Una escuadra es un grupo de personas que trabajan juntas para lograr un objetivo común. Para poder sacar una escuadra, es necesario tomar ciertas medidas para asegurar que todos los miembros estén alineados y comprometidos.
En primer lugar, es fundamental establecer metas claras y objetivos específicos para la escuadra. Esto ayudará a mantener el enfoque y a guiar las acciones de todos los miembros. Además, es importante que estos objetivos sean medibles y que se puedan evaluar en el transcurso del tiempo.
Para lograr la coordinación y el trabajo en equipo necesario para sacar una escuadra, es esencial establecer roles y responsabilidades claras para cada miembro. Esto asegurará que cada individuo comprenda su parte en el conjunto y pueda contribuir de manera efectiva.
Otra medida importante es fomentar la comunicación abierta y efectiva dentro de la escuadra. Esto implica crear un ambiente donde todos se sientan cómodos para expresar sus ideas, compartir información y resolver conflictos de manera constructiva. La comunicación regular y constante ayudará a mantener a todos al tanto de los avances y desafíos que enfrenta la escuadra.
Además, es fundamental establecer un sistema de seguimiento y evaluación para evaluar el desempeño de la escuadra. Esto permitirá identificar áreas de mejora y tomar acciones correctivas cuando sea necesario. También se pueden implementar incentivos y recompensas para reconocer y motivar el buen desempeño dentro de la escuadra.
En resumen, sacar una escuadra implica tomar medidas como establecer metas claras, definir roles y responsabilidades, fomentar la comunicación abierta y efectiva, y establecer un sistema de seguimiento y evaluación. Estas medidas ayudarán a garantizar el éxito y lograr los objetivos establecidos por la escuadra.
¿Qué medidas se dan para sacar una escuadra?
La escuadra es un instrumento de geometría utilizado para trazar y medir ángulos rectos. Para poder utilizar correctamente una escuadra, se deben tomar en cuenta ciertas medidas. A continuación, se detallarán las principales medidas que se deben dar para sacar una escuadra.
En primer lugar, es necesario colocar la escuadra sobre la hoja de papel o superficie donde se va a trabajar. Se debe asegurar que uno de los lados de la escuadra quede alineado con algún borde de referencia, como el borde de la hoja o el borde de la mesa. Esto permitirá que los ángulos se tracen de manera precisa y se obtengan resultados más exactos.
Una vez colocada la escuadra, se debe buscar el ángulo de 90 grados. Este es el ángulo recto y la razón principal por la que se utiliza una escuadra. Para encontrarlo, se utiliza el lado recto de la escuadra. Se debe asegurar que este lado recto esté perfectamente alineado con el borde de la hoja o superficie, para asegurar la precisión del ángulo.
Otra medida importante para sacar una escuadra es la longitud de los lados. Esto se refiere a la medida de los dos lados de la escuadra, excluyendo el lado recto. La longitud de los lados puede variar dependiendo del tamaño y tipo de escuadra utilizada. Es importante verificar que los lados de la escuadra sean iguales en longitud para obtener resultados precisos.
Además de estas medidas, es fundamental tener en cuenta la posición y el ángulo de visión. La escuadra debe estar colocada correctamente frente al ojo del observador, de manera que los resultados sean percibidos de la manera más exacta posible. Además, se debe mirar desde un ángulo perpendicular a la escuadra para evitar distorsiones en las mediciones.
En resumen, para sacar una escuadra correctamente se deben tomar medidas precisas al colocarla sobre la superficie de trabajo, encontrar el ángulo de 90 grados, verificar la longitud de los lados y considerar la posición y el ángulo de visión. Estas medidas permitirán obtener resultados exactos y utilizar la escuadra de manera efectiva en trabajos de geometría y diseño.
¿Qué es el Método 3 4 y 5?
El Método 3-4-5 es una técnica utilizada para resolver problemas de medición y cálculo en áreas de construcción y diseño. Este método se basa en la relación entre los lados de un triángulo rectángulo.
El nombre del método se debe a que utiliza los números 3, 4 y 5 para establecer una proporción entre los lados de un triángulo rectángulo. Estos números representan los valores de las longitudes de los lados del triángulo en unidades de medida determinadas.
La clave del Método 3-4-5 es que se basa en el teorema de Pitágoras, que establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Así, utilizando las proporciones del 3-4-5, es posible calcular la longitud de los lados de un triángulo rectángulo sin necesidad de realizar mediciones directas.
Este método es muy útil en la construcción, especialmente al realizar trabajos de nivelación y trazado de ángulos rectos. Por ejemplo, si necesitamos asegurarnos de que una pared esté perfectamente perpendicular al suelo, podemos utilizar el Método 3-4-5 para trazar un triángulo rectángulo con las medidas correctas y asegurarnos de que los ángulos del triángulo sean de 90 grados.
En resumen, el Método 3-4-5 es una herramienta práctica y precisa para realizar mediciones y cálculos en el campo de la construcción y el diseño. Al utilizar una proporción basada en los números 3, 4 y 5, es posible calcular la longitud de los lados de un triángulo rectángulo de manera rápida y precisa, lo que permite agilizar los trabajos de construcción y asegurar la precisión en el trazado de ángulos rectos.
¿Cuánto miden los ángulos de una escuadra?
¿Cuánto miden los ángulos de una escuadra? Esta pregunta es común cuando se trata de geometría. Una escuadra es una herramienta muy utilizada en matemáticas y dibujo técnico, compuesta por dos brazos perpendiculares entre sí. Estos brazos forman dos ángulos rectos.
Un ángulo recto tiene una medida de 90 grados. Por lo tanto, podemos decir que los dos ángulos formados por una escuadra miden siempre 90 grados cada uno.
Esta medida es constante y se aplica a cualquier escuadra, sin importar su tamaño. Ya sea una escuadra pequeña o una escuadra grande, ambos ángulos internos siempre tendrán una medida de 90 grados.
Esto es muy útil al dibujar líneas perpendiculares o ángulos rectos en un plano. La escuadra proporciona una referencia precisa para asegurarse de que los ángulos sean exactamente de 90 grados.
Además de los ángulos rectos que forman las dos ramas de la escuadra, también podemos encontrar otros ángulos en esta herramienta. Por ejemplo, si trazamos una línea oblicua a través de la escuadra, se formarán ángulos agudos o ángulos obtusos.
Los ángulos agudos miden menos de 90 grados, mientras que los ángulos obtusos miden más de 90 grados. Estos ángulos pueden variar de una escuadra a otra, dependiendo de su diseño y tamaño.
En resumen, los ángulos de una escuadra siempre miden 90 grados, lo que hace de esta herramienta una pieza fundamental en el dibujo técnico y la geometría. Su diseño de dos ramas perpendiculares permite trazar líneas perpendiculares y ángulos rectos con precisión.
¿Qué es una escuadra de albañil?
Una escuadra de albañil es una herramienta esencial en la construcción y albañilería.
Se trata de una regla metálica con forma de triángulo rectángulo, donde sus dos lados más pequeños son perpendiculares entre sí.
La escuadra de albañil se utiliza para medir, marcar y comprobar ángulos rectos en las construcciones.
Este instrumento permite a los albañiles asegurarse de que las esquinas de las paredes, techos y suelos están perfectamente perpendiculares.
La escuadra de albañil también es útil para confirmar que las líneas y los cortes que se realizan en los materiales de construcción son rectos y precisos.
La mayoría de las escuadras de albañil tienen medidas estándar, como 30 centímetros en uno de los lados más largos y 40 centímetros en el otro lado.
Estas herramientas suelen estar hechas de metal resistente, como el acero inoxidable, para garantizar su durabilidad.
Algunas escuadras de albañil también cuentan con marcas y grabados que facilitan la medición y la alineación de las piezas durante la construcción.
En resumen, una escuadra de albañil es una herramienta clave para los profesionales de la construcción, ya que les ayuda a medir, marcar y comprobar ángulos rectos en sus proyectos.
Escuadra
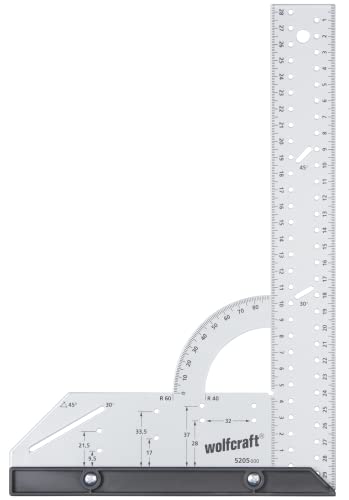
wolfcraft Escuadra universal, 5205000, Para medir, trazar, dibujar y hacer cortes guiados
- Ángulo plano, escala de medición angular, trazador paralelo, patrón trazador y guía de orificios para bisagras tipo cazoleta en un solo aparato
- Tope de plástico extraíble para un trazado preciso en la superficie o el canto
- Modelo de metal de calidad con graduación en ambos lados
- Marca: Wolfcraft


Escuadra carpintero,180 mm Escuadras Metalicas,Multifuncional Regla Triangular Métrica de Aluminio,Herramientas de Carpintero para Medir, Marcar, Cortar,herramientas bricolaje
- Material de alta calidad: hecho de aleación de aluminio de alta calidad, alta dureza, negro mate, buena mano de obra, prevención efectiva de la reflexión de luz fuerte, no es fácil de oxidar y desgastar, no es fácil de romper, sólido y duradero. Adecuado para carpintería, marcos, regulaciones de ángulo, juntas oblicuas, almohadillas, guías de sierra, soportes de carpintería y guías de corte de bordes
- Ahorro de tiempo: el ángulo métrico es la regla, el ángulo de parada, el itinerario y el ángulo. Con esta herramienta de carpintería, ahorras mucho tiempo y energía. La perspectiva general que ofrecemos para su proyecto. La fabricación precisa del ángulo del Carpintero garantiza una medición precisa del ángulo y la longitud, en milímetros y centímetros.
- ¡Trabajo eficiente: Grupo de reglas, contorno de ángulo, regla de vernier, regla de ángulo y ayuda de perforación - ¡ la herramienta de carpintería más universal! ¡¡ herramientas sólidas marcadas por perforación, alta precisión milimétrica y fuerte practicidad! ¡¡ herramientas de carpintería multifuncionales! Es muy adecuado para 10 aplicaciones, como vías de madera, nivelación y búsqueda de laderas en techos.
- Imprescindible profesional: muy adecuado para profesionales y hágalo usted mismo, es imprescindible para cualquier caja de herramientas. El Centro del triángulo del carpintero es un marco gráfico auxiliar hueco que le permite dibujar líneas y gráficos rápidamente en la tabla, y los bordes fijos prácticos se pueden conectar a la tabla, por lo que puede hacer fácilmente cortes horizontales o oblicuos sin moverse a la izquierda y a la derecha. Mejorar la precisión de Corte.
- Regalo: esta herramienta multifuncional hace que su trabajo sea más fácil y es un regalo artesano ideal. Es probable que tu amada lo haga él mismo, pero aún no tiene herramientas de medición y planificación en el sitio de construcción. ¡¡ este cuerno metálico con plantilla de agujero es un hermoso regalo de herramientas de madera que complacerá a profesionales y entusiastas del bricolaje!

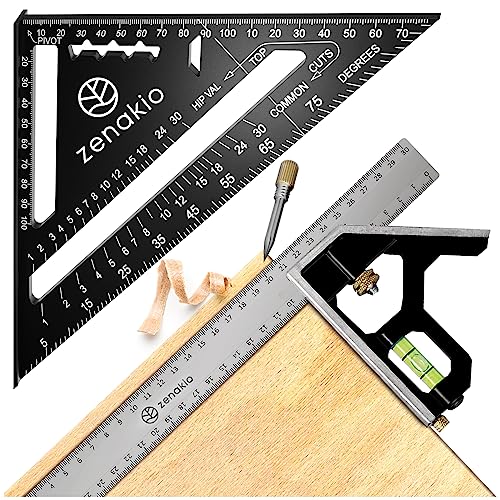
Zenakio Escuadra Carpintero 12-EN-1 - Kit Completo Escuadras Metalicas Carpintero (set de 2) - Escuadra Metalica 185mm + Herramienta de Medir 300mm - Escuadra Combinada 1 Para Bricolaje
- EL KIT 12-EN-1: El kit de escuadra de carpintero Zenakio es multifuncional: transportador de angulos, regla rodante profesional, plantilla de corte, herramienta de trazado, gramil; es el set perfecto de bricolaje profesional ¡Perfecto tanto para los profesionales como para los manitas, este kit te acompaña para trabajar la madera de una manera rápida y precisa! Nuestro kit está formado por una escuadra de carpinteria + escuadra combinada + manual
- ESCUADRA Y CARTABON - 185mm: Metalica de alta calidad, 100% aluminio, te guía en tus cortes con sierra - Es polivalente: regla, transportador de angulo, gramil, escuadra de angulo - Con una longitud de 18,5 cm, la escuadra y cartabon metalico es práctica y duradera: usa el punto de pivote, el transportador, la regla multifuncional deslizante para medir los ángulos y la guía y el gramil para trazar las rectas ¡La tabla de conversión te permite trabajar con cm e inch!
- ESCUADRA COMBINADA CON CABEZAL CUADRADO AJUSTABLE: De acero inoxidable premium, está compuesta por una regla metalica de 300mm, un cabezal cuadrado con tuerca ajustable firme y precisa, unas escuadras angulo 45º y 90º, un gramil para carpintero y mini nivel burbuja resistente a los golpes; La escuadra con medidor de angulo te brinda un amplio abanico de usos, esta herramienta de medir permite un trazado y una medición precisa de ángulos, haz tus tareas de bricolaje con total sencillez
- MEDICIONES MULTIDIMENSIONALES PRECISAS: Gracias a tus herramientas carpinteria Zenakio, marca rápidamente tus líneas de corte y corta con precisión. La tabla de conversión CM/Inch simplifica tu trabajo y te brinda una medición polivalente gracias a las equivalencias - Disfruta de una medición multifuncional: nivel, medida de ángulos a 90º, 45º; puede servir de indicador de pestaña, de altura o de profundidad
- MÁXIMA RAPIDEZ: Gracias a tu escuadra universal + regla triangular, ¡gana rapidez en tu trabajo con la madera y en tus obras! El kit de herramientas de carpinteria te permite ir mucho más rápido a la hora de medir y trazar ángulos o tomar medidas precisas fácilmente - Perfecto tanto para profesionales como para manitas, regala este objeto imprescindible entre las herramientas bricolaje profesional: incluye un manual de uso con vídeos tutoriales para acompañarte en tus tareas


Escuadra Carpintero 180mm, Escuadra Combinada 300mm, Metalicas Carpintero con Nivel de Burbuja,Lápiz Metálico e 12 minas de lápiz para carpintero medir y marcar
- 【Juego de Reglas de ángulos de Carpintero】: El Carpenter's Angle Ruler Set contiene una regla triangular y una combinación de ángulos, así como un lápiz con 12 recambios de lápiz de diferentes colores para usar en diferentes objetos. Regla de Triángulo es la herramienta perfecta para que pueda medir y marcar objetos con precisión para satisfacer sus diferentes necesidades.
- 【Regla Triangular Engrosada】: Regla Escuadra Combinada tiene una longitud total de medición de 18 cm y puede medir de 0 ° a 90 °, también puede dibujar líneas horizontales, ángulos iguales y líneas verticales paralelas, con agujeros de 3-15 mm de diámetro para un trabajo de perforación sencillo y rápido, así como establecer dentados y dibujar círculos para marcar tableros de dibujo.
- 【Regla de ángulos Combinada con Tuerca Ajustable】: La Escuadra Metalica tiene una longitud de medición completa de 30 cm y puede medir ángulos de 45 ° la tuerca en la parte superior es ajustable y se puede mover a voluntad,lo que hace que la medición sea más conveniente. La burbuja horizontal del Regla Escuadra Combinada es menos probable que se escape, ayudando a una medición más precisa,El pasador de trazado oculto en la parte inferior es un diseño extraíble que no se raya cuando se utiliza.
- 【Material de Alta Calidad y Duradero】: Regla de Triángulo está hecho de aleación de aluminio de alta calidad, alta dureza, resistencia a la corrosión, no es fácil de oxidar y desgastar, robusto y duradero, escalas delantera y trasera claras y nítidas, proceso de láser negro, previene eficazmente la reflexión, la burbuja horizontal fluorescente de Cuadrado de Carpintero no es fácil de filtrar.
- 【Ampliamente Utilizado】:Regla Escuadra Combinada de Carpintero es ampliamente aplicable, adecuado para herramientas de medición de marcado de madera, puede ayudarlo a medir desde múltiples ángulos, Escuadra de Carpintero Profesional es conveniente y práctico, herramienta de medición multifuncional, ahorre su tiempo y mejore la eficiencia del trabajo.

